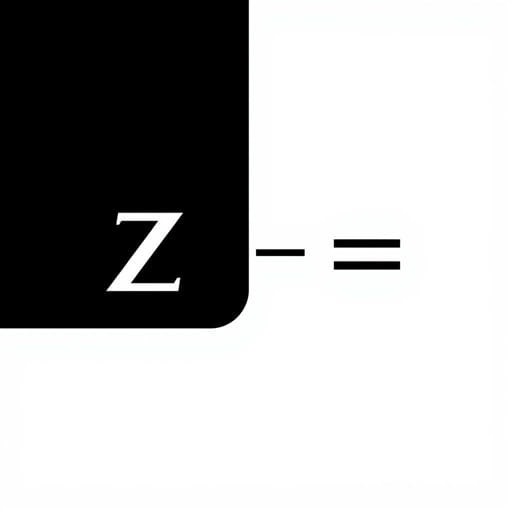In fluid mechanics, the Bernoulli equation is a fundamental principle that explains the behavior of fluid flow, pressure, and velocity along a streamline. Among the terms in the Bernoulli equation, the variable z” often appears, representing an essential concept that links fluid dynamics with gravitational potential energy. Understanding “z” in the context of the Bernoulli equation is crucial for engineers, physicists, and anyone studying fluid systems because it provides insight into how the height or elevation of a fluid affects pressure and velocity. This knowledge is widely applied in designing pipelines, hydraulic systems, and even in understanding natural phenomena such as river flow and atmospheric pressure variations.
Introduction to the Bernoulli Equation
The Bernoulli equation is derived from the principle of conservation of energy applied to flowing fluids. It states that the total mechanical energy along a streamline remains constant for an incompressible, non-viscous fluid in steady flow. The equation is usually expressed as
P + ½ρv² + ρgz = constant
Here, P represents the fluid pressure, ρ is the fluid density, v is the fluid velocity, g is the acceleration due to gravity, and z represents the elevation of the fluid above a reference point. Each term in the equation corresponds to a type of energy pressure energy, kinetic energy, and potential energy due to elevation. Among these, the term ρgz, where z appears, specifically accounts for the gravitational potential energy of the fluid.
Understanding the Term “z”
The variable “z” in the Bernoulli equation represents the height or elevation of a point in the fluid relative to a chosen reference plane, often called the datum. It quantifies the potential energy per unit weight of the fluid due to gravity. In practical terms, the higher the fluid is above the reference point, the larger the value of z, and consequently, the greater the potential energy contribution to the total energy in the Bernoulli equation. This concept is particularly important in engineering applications where elevation differences influence fluid behavior, such as in water supply systems, dams, or aircraft hydraulics.
Physical Significance of “z”
The elevation term z plays a critical role in analyzing fluid systems where height differences are significant. It reflects how gravitational forces affect the pressure and velocity of a fluid. For example, when a fluid flows from a higher elevation to a lower one, the potential energy represented by ρgz decreases. This energy can be converted into kinetic energy, increasing the velocity of the fluid, or it can increase the fluid pressure, depending on the system configuration. Understanding this conversion is essential for predicting fluid behavior accurately.
Application of “z” in Fluid Systems
The term “z” is widely used in practical applications to calculate pressures and velocities in systems with varying elevations. Engineers often need to account for elevation differences to design pumps, pipelines, and open channels efficiently. Some typical applications include
- Pipelines and Water DistributionThe elevation term is crucial when designing water supply systems, as the pressure must be sufficient to deliver water to higher floors or distant locations.
- Hydraulic DamsThe potential energy represented by z helps in calculating the energy available for turbines to generate electricity in hydroelectric plants.
- AerodynamicsIn some cases, changes in elevation affect the pressure distribution around aircraft surfaces or wind turbines, indirectly influencing the performance of these systems.
Choosing a Reference Point
When applying the Bernoulli equation, the elevation z is always measured from a reference point or datum. The choice of this reference does not affect the physical behavior of the fluid, as only differences in z between points influence pressure and velocity changes. Engineers commonly select the lowest point in the system as the reference to simplify calculations, though any consistent plane can be used. This flexibility allows for easier analysis of complex fluid systems.
Relationship Between z and Other Bernoulli Terms
The elevation term z interacts with pressure and velocity terms to maintain the total energy balance along a streamline. If the height of the fluid increases, the potential energy term ρgz increases, which can result in a decrease in pressure or velocity if no external energy is added to the system. Conversely, if the fluid flows downward, the reduction in z leads to increased velocity or pressure. This interplay is critical in understanding phenomena such as siphons, open-channel flow, and pipe networks where both elevation and pressure differences drive fluid movement.
Example Calculations Involving “z”
To illustrate the significance of z, consider a water tank elevated above a ground-level pipe. Using the Bernoulli equation, engineers can calculate the pressure at the pipe outlet, accounting for the height of the water surface. The ρgz term represents the potential energy due to the water’s elevation, which contributes to the pressure that forces water through the pipe. Similarly, in a hydroelectric dam, the height of water above turbines directly determines the potential energy available for power generation, calculated using the same principle.
Practical Considerations
In real-world applications, it is important to note that the Bernoulli equation assumes an ideal fluid, meaning no viscosity or energy losses. In practice, energy losses due to friction, turbulence, and other factors must be considered. Even with these limitations, the elevation term z remains a fundamental part of fluid analysis, providing insight into the role of gravity in energy distribution along a fluid path.
The variable z in the Bernoulli equation represents the elevation or height of a fluid point relative to a reference plane and is directly tied to the fluid’s gravitational potential energy. Understanding this term is essential for analyzing how fluids behave in systems with varying elevations, predicting pressure and velocity changes, and designing efficient hydraulic and fluid transport systems. Whether in pipelines, dams, or open-channel flows, the elevation term helps quantify the effect of gravity on fluid motion, allowing engineers and scientists to apply the principles of energy conservation effectively. By considering z alongside pressure and velocity terms, one gains a complete picture of energy distribution in fluid systems, making it a cornerstone concept in fluid mechanics and engineering applications.